MODELOS DE PROBABILIDAD III      

DISTRIBUCIÓN DE POISSON DISTRIBUCIÓN EXPONENCIAL DISTRIBUCIÓN UNIFORME DISCRETA DISTRIBUCIÓN  UNIFORME CONTINUA

ir a modelos       imprimir en PDF parteIII

    Esta distribución es una de las más importantes distribuciones de variable discreta. Sus principales aplicaciones hacen referencia a la modelización de situaciones en las que nos interesa determinar el número de hechos de cierto tipo que se pueden producir en un intervalo de tiempo o de espacio, bajo presupuestos de aleatoriedad y ciertas circunstancias restrictivas. Otro de sus usos frecuentes es la consideración límite de procesos dicotómicos reiterados un gran número de veces si la probabilidad de obtener un éxito es muy pequeña .   ir a programa de cálculo

Proceso experimental del que se puede hacer derivar

    Esta distribución se puede hacer derivar de un proceso experimental de observación en el que tengamos las siguientes características

· Se observa la realización de hechos de cierto tipo durante un cierto periodo de tiempo o a lo largo de un espacio de observación

· Los hechos a observar tienen naturaleza aleatoria ; pueden producirse o no de una manera no determinística.

· La probabilidad de que se produzcan un número x de éxitos en un intervalo de amplitud t no depende del origen del intervalo (Aunque, sí de su amplitud)

· La probabilidad de que ocurra un hecho en un intervalo infinitésimo es prácticamente proporcional a la amplitud del intervalo.

· La probabilidad de que se produzcan 2 o más hechos en un intervalo infinitésimo es un infinitésimo de orden superior a dos.

· Si en estas circunstancias aleatorizamos de forma que la variable aleatoria X signifique o designe el "número de hechos que se producen en un intervalo de tiempo o de espacio", la variable X se distribuye con una distribución de parámetro l . Así :          

    El parámetro de la distribución es, en principio, el factor de proporcionalidad para la probabilidad de un hecho en un intervalo infinitésimo. Se le suele designar como parámetro de intensidad , aunque más tarde veremos que se corresponde con el número medio de hechos que cabe esperar que se produzcan en un intervalo unitario (media de la distribución); y que también coincide con la varianza de la distribución.

    Por otro lado es evidente que se trata de un modelo discreto y que el campo de variación de la variable será el conjunto de los número naturales, incluido el cero:    

        A partir de las hipótesis del proceso, se obtiene una ecuación diferencial de definición del mismo que puede integrarse con facilidad para obtener la función de cuantía de la variable "número de hechos que ocurren en un intervalo unitario de tiempo o espacio "

                                                              Que sería :             ir a programa de cálculo

Cuya representación gráfica para un modelo de media 11 sería la adjunta .
Obsérvense los valores próximos en la media y su forma parecida a la campana de Gauss , en definitiva , a la distribución normal

            La función de distribución vendrá dada por :

           Su expresión será :          

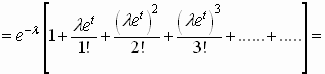
                             dado que tendremos que   

                                                       luego :     

Para la obtención de la media y la varianza aplicaríamos la F.G.M.; derivándola sucesivamente e igualando t a cero .

Así.

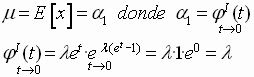
                             Una vez obtenida la media , obtendríamos la varianza en base a :

                                                                           haciendo t = 0
                                                                                               

                                                   por lo que =

                                         así se observa que media y varianza coinciden con el parámetro del modelo siendo , l

    En cuanto a la moda del modelo tendremos que será el valor de la variable que tenga mayor probabilidad , por tanto si Mo es el valor modal se cumplirá que :

                           Y, en particular:

    A partir de estas dos desigualdades, es muy sencillo probar que la moda tiene que verificar: De manera que la moda será la parte entera del parámetro l o dicho de otra forma, la parte entera de la media

    Podemos observar cómo el intervalo al que debe pertenecer la moda tiene una amplitud de una unidad , de manera que la única posibilidad de que una distribución tenga dos modas será que los extremos de este intervalo sean números naturales, o lo que es lo mismo que el parámetro l sea entero, en cuyo caso las dos modas serán l -1 y l .

La distribución de Poisson verifica el teorema de adición para el parámetro l .

"La variable suma de dos o más variables independientes que tengan una distribución de Poisson de distintos parámetros l (de distintas medias) se distribuirá, también con una distribución de Poisson con parámetro l la suma de los parámetros l (con media, la suma de las medias) :

En efecto:

Sean x e y dos variables aleatorias que se distribuyen con dos distribuciones de Poisson de distintos parámetros siendo además x e y independientes

Así e

        Debemos probar que la variable Z= x+y seguirá una Poisson con parámetro igual a la suma de los de ambas:             

                       En base a las F.G.M para X     

                                                            Para Y

 De manera que la función generatriz de momentos de Z será el producto de ambas ya que son independientes :

             Siendo                   la F.G.M de una Poisson

    Se puede probar que la distribución binomial tiende a converger a la distribución de Poisson cuando el parámetro n tiende a infinito y el parámetro p tiende a ser cero, de manera que el producto de n por p sea una cantidad constante. De ocurrir esto la distribución binomial tiende a un modelo de Poisson de parámetro l igual a n por p

Este resultado es importante a la hora del cálculo de probabilidades , o , incluso a la hora de inferir características de la distribución binomial cuando el número de pruebas sea muy grande y la probabilidad de éxito sea muy pequeña .

        El resultado se prueba , comprobando como la función de cuantía de una distribución binomial con y tiende a una función de cuantía de una distribución de Poisson con   siempre que este producto sea una cantidad constante ( un valor finito)

                En efecto : la función de cuantía de la binomial es

                Y llamamos tendremos que:

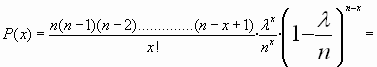
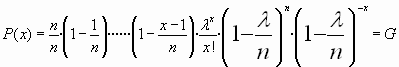
                realizando que es la función de cuantía de una distribución de Poisson

    Análogamente a como planteábamos el problema de necesitar estimar la proporción de una característica ,en el caso de un modelo binomial , en alguna situación práctica , podemos estar interesados en determinar el parámetro desconocido de una distribución de Poisson. Por ejemplo podríamos estar interesados en determinar el número medio de clientes que acuden a una ventanilla de una oficina pública.

    El planteamiento de la estimación podría hacerse utilizando información suministrada por una experiencia {la observación de cuántos hechos se producen en un intervalo experimental),conjuntamente con algún otro tipo de información a priori .En este caso, estaríamos ,como ya comentábamos en el caso binomial ante un planteamiento bayesiano del problema.

    La solución requerirá que dispongamos de una información inicial que puede especificarse a través de una distribución a priori de probabilidad. De manera que la función de cuantía de esta distribución a priori (o su f. de densidad si fuera continua) nos asigne probabilidades a cada posible valor del parámetro l .

Utilizando únicamente la información inicial la estimación sería la media de la distribución a priori.

    Pero realizando una experiencia podremos mejorar la información acerca de l Si observamos la realización de hechos durante un intervalo experimental y se producen x hechos, para cada posible valor de l podremos calcular su verosimilitud definida como la probabilidad de que se dé ese resultado si el valor de l es el considerado:

    Obviamente esta probabilidad condicionada será la función de cuantía de una distribución de Poisson con . para el valor de la variable x.

    Finalmente podemos calcular las probabilidades de cada valor alternativo de , condicionada al resultado de la experiencia aplicando el teorema de Bayes:

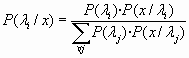
    Estas probabilidades finales (a posteriori) constituirán la función de cuantía de la distribución a posteriori que nos dará cuenta de toda la información disponible (tanto muestral como no muestral) .

    La estimación mejorada del parámetro será, entonces, la media de la distribución a posteriori.

Planteamos un ejemplo:

    Tres ejecutivos del Insalud opinan que el número medio de pacientes que llegan a cierto servicio nocturno de guardia durante una hora es 2 , según el primero, 3 , según el segundo, y 5 según el tercero.

    Sus opiniones pueden ponderarse teniendo en cuenta que el primero tiene el doble de experiencia profesional que los otros dos.

    Para tomar una decisión de asignación de personal en ese servicio quieren estimar el número medio de pacientes, sin despreciar sus opiniones , por lo que realiza una experiencia controlando una hora de actividad en el servicio en la que acuden 3 pacientes .Esta información la van a combinar con la inicial a través de un proceso Bayesiano :¿cómo lo harían?

La distribución a priori será tal que deberá asignarse el doble de probabilidad a la alternativa propuesta por el primer experto que a las de los otros dos. Así que será:

De manera que la estimación inicial de sería,la media de la distribución a priori:

Realizada la experiencia, las verosimilitudes de las tres alternativas nos vendrán dadas por la función de cuantía de la distribución de Poisson, con

La función de cuantía de la distribución a posteriori la obtendremos aplicando el Teorema de Bayes y resultará ser:

Esta distribución a posteriori nos dará cuenta de toda la información disponible acerca del parámetro desconocido, (número medio de pacientes por hora); tanto de la información subjetiva de los expertos (convenientemente ponderada) como de la información empírica suministrada por la observación.

A partir de esta distribución a posteriori podemos plantear nos dar un valor concreto para la estimación de considerando una función de pérdida cuadrática . La estimación adecuada sería la media de la distribución a posteriori:

                                                                       
                                                                                              pacientes la hora

    A pesar de la sencillez analítica de sus funciones de definición, la distribución exponencial tiene una gran utilidad práctica ya que podemos considerarla como un modelo adecuado para la distribución de probabilidad del tiempo de espera entre dos hechos que sigan un proceso de Poisson. De hecho la distribución exponencial puede derivarse de un proceso experimental de Poisson con las mismas características que las que enunciábamos al estudiar la distribución de Poisson, pero tomando como variable aleatoria , en este caso, el tiempo que tarda en producirse un hecho

Obviamente, entonces , la variable aleatoria será continua. Por otro lado existe una relación entre el parámetro a de la distribución exponencial , que más aparecerá , y el parámetro de intensidad del proceso l , esta relación es a = l

Al ser un modelo adecuado para estas situaciones tiene una gran utilidad en los siguientes casos:

· Distribución del tiempo de espera entre sucesos de un proceso de Poisson

· Distribución del tiempo que transcurre hasta que se produce un fallo, si se cumple la condición que la probabilidad de producirse un fallo en un instante no depende del tiempo transcurrido .Aplicaciones en fiabilidad y teoría de la supervivencia.

    A pesar de lo dicho sobre que la distribución exponencial puede derivarse de un proceso de Poisson , vamos a definirla a partir de la especificación de su función. de densidad:

    Dada una variable aleatoria X que tome valores reales no negativos {x ³ 0} diremos que tiene una distribución exponencial de parámetro a con a ³ 0, si y sólo si su función de densidad tiene la expresión:

                                                                        Diremos entonces que

Gráficamente como ejemplo planteamos el modelo con parámetro a =0,05

                                    En consecuencia , la función de distribución será:

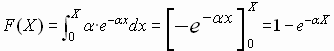
    En la principal aplicación de esta distribución , que es la Teoría de la Fiabilidad, resulta más interesante que la función de distribución la llamada Función de Supervivencia o Función de Fiabilidad.

                La función de Supervivencia se define cómo la probabilidad de que la variable aleatoria tome valores superiores al valor dado X:

        Si el significado de la variable aleatoria es "el tiempo que transcurre hasta que se produce el fallo": la función de distribución será la probabilidad de que el fallo ocurra antes o en el instante X: y , en consecuencia la función de supervivencia será la probabilidad de que el fallo ocurra después de transcurrido el tiempo X ; por lo tanto, será la probabilidad de que el elemento, la pieza o el ser considerado "Sobreviva" al tiempo X ; de ahí el nombre.

Gráficamente, la función de distribución para un modelo exponencial de parámetro a =0,05 sería :

En la que se observa lo que sería la diferencia entre función de distribución y la de supervivencia

                La Función Generatriz de Momentos será :

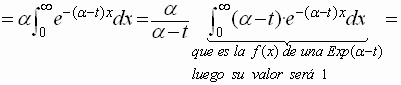
                                      tendremos así que la F.G.M será :

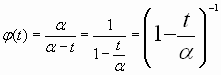
    Una vez calculada la F.G.M podemos , partiendo de ella , calcular la media y la varianza

                Así la media será:

               En cuando a la varianza su expresión será :

ya que

        La mediana del modelo exponencial será aquel valor de la variable x =Me que verifica que F(Me) = ½

                            De manera que por lo que

    Dentro del marco de la teoría de la fiabilidad si un elemento tiene una distribución del tiempo para un fallo con una función de densidad f(x) , siendo x la variable tiempo para que se produzca un fallo , y con una función de supervivencia S(X) La probabilidad de que un superviviente en el instante t falle en un instante posterior t + D t será una probabilidad condicionada que vendrá dada por:

    Al cociente entre esta probabilidad condicionada y la amplitud del intervalo considerado, t , se le llama tasa media de fallo en el intervalo [t , t+D t] :

Y a la tasa media de fallo en un intervalo infinitésimo es decir, al límite de la tasa media de fallo cuando D t® 0 se le llama Tasa Instantánea de Fallo (o, simplemente, tasa de fallo) en t:

            La tasa de fallo es, en general, una función del tiempo, que define unívocamente la distribución.

        Pues bien, puede probarse que el hecho de que la tasa de fallo sea constante es condición necesaria y suficiente para que la distribución sea exponencial y que el parámetro es, además, el valor constante de la tasa de fallo.

en efecto:

                                si

                de donde integrando esta ecuación diferencial entre 0 y x :

                            de modo que la función de distribución será

                                                         Función de Distribución de una Exponencial

                    Si X tiene una distribución exponencial

                                                    de manera que

        Así pues si un elemento tiene una distribución de fallos exponencial su tasa de fallos se mantiene constante a lo largo de toda la vida del elemento. La probabilidad de fallar en un instante no depende del momento de la vida del elemento en el que nos encontremos; lo que constituye la propiedad fundamental de la distribución que ahora enunciamos:

La distribución exponencial no tiene memoria :

    Poseer información de que el elemento que consideramos ha sobrevivido un tiempo S (hasta el momento) no modifica la probabilidad de que sobreviva t unidades de tiempo más. La probabilidad de que el elemento falle en una hora (o en un día, o en segundo) no depende del tiempo que lleve funcionando. No existen envejecimiento ni mayor probabilidad de fallos al principio del funcionamiento

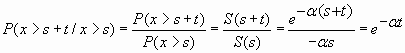
                                    Expresión que no depende , como se observa , del tiempo sobrevivido s.

    Es una distribución muy sencilla que asigna probabilidades iguales a un conjunto finito de puntos del espacio.

     Modeliza fenómenos en los que tenemos un conjunto de n sucesos posibles, cada uno de los cuales con la misma probabilidad de ocurrir. Si aleatorizamos de forma que cada uno de éstos sucesos se corresponda con un número natural del 1 al n obtendremos una distribución uniforme. Tendremos un único parámetro ; n

                                    Diremos , por tanto que 
                                                                             

    Puede hacerse derivar en consecuencia de un proceso experimental de selección aleatoria, en el que la característica que consideramos en la selección sólo puede tomar un conjunto de n valores discretos y donde cualquiera de estos valores puede obtenerse con igual probabilidad.

        Por su elementaridad  no es una distribución de excesivo interés práctico.

        Su función de cuantía definida para los valores de x ={ 1, 2,    , n} vendrá dada por la constante:
                  P(x) = l /n  para x ={ 1, 2,      , n}
Su función de distribución vendrá dada por 

                           Puede comprobarse que su media será

                       

                                              su varianza será :    

                        por último,  su Función Generatriz de Momentos, quedará expresada como
                                                        

 DISTRIBUCIÓN UNIFORME (DE V.CONTINUA)

La distribución o modelo uniforme puede considerarse como proveniente de un proceso de extracción aleatoria .El planteamiento radica en el hecho de que la probabilidad se distribuye uniformemente a lo largo de un intervalo . Así : dada una variable aleatoria continua, x , definida en el intervalo [a,b] de la recta real, diremos que x tiene una distribución uniforme en el intervalo [a,b] cuando su función de densidad para sea: para x Î [a,b].

Su representación gráfica será :

De manera que la función de distribución resultará:

Su representación gráfica será :

Este modelo tiene la característica siguiente : Si calculamos la probabilidad del suceso
                                                                       

                                Tendremos:

                Este resultado nos lleva a la conclusión de que la probabilidad de cualquier suceso depende únicamente de la amplitud del intervalo (D X) , y no de su posición en la recta real [a , b] . Lo que viene ha demostrar el reparto uniforme de la probabilidad a lo largo de todo el campo de actuación de la variable , lo que , por otra parte, caracteriza al modelo.

En cuanto a las ratios de la distribución tendremos que la media tiene la expresión:

La varianza tendrá la siguiente expresión:

                                                de donde

                                        por lo que

La función generatriz de momentos vendrá dada por :

Lógicamente partiendo de esta función podríamos recalcular media y varianza gracias al teorema de los momentos

ir a modelos de probabilidad